[译] 关于Javascript的Number类型，你需要知道的东西

Posted on |
关于Javascript的Number类型，你需要知道所有的东西都在这里！浮点数如何表示？为什么0.1+0.2不等于0.3？9007199254740992 为什么等于 9007199254740993， 不是道德的沦丧，也不是人性的扭曲！

原文地址： https://medium.com/dailyjs/javascripts-number-type-8d59199db1b6

为什么0.1+0.2不等于0.3， 而9007199254740992 等于 9007199254740993

大多数静态语言的数字都有不同的数据类型，比方说你想保存一个在[-128; 127]之间的整数，C语言你可以用char，Java可以用byte，他们都占用一个字节。如果你要存储一个大的数字，你可以使用4字节的int或者8字节的long。这些语言对带小数的数字同样有其特殊的数据类型，譬如4字节的float和8字节的double。这两种类型一般都称为浮点类型，后面我们会知道这个名字的缘来。

但是在Javascript中，我们没有那么多的类型。根据ECMAScript标准，数字只有一种类型，即双精度，64位二进制，符合IEEE 754格式的值。这种类型和C与Java的double类型一样，用于存储整数和小数。一些js的开发者没有意识到这一点，于是觉得1是这样存储的：

然而，实际上是存成这样子的：

这个误解可能引起很大的困惑，比方说下面这个Java的循环

1
2
3
for (int i=1; 1/i > 0; i++) {
    System.out.println("Count is: " + i);
}

我们很容易知道它是怎么结束循环的，第二次循环迭代的是会后i变成2，然后1/2等于0.5,因为是int类型，结果被截断为0。循环结束。

现在想象下同样的循环跑在Javascript下：

1
2
3
for (var i=1; 1/i > 0; i++) {
    console.log("Count is: " + i);
}

这是个死循环(╯﹏╰)，因为1/i不会得到一个整数，而是一个浮点数。想知道为啥不，继续往下阅读把💯

另外一个不熟悉Javascript的人会经常提的问题是0.1加0.2等于0.30000000000000004, 这意味着0.1加0.2不等于0.3。stackoverflow上面有许多这个现象的问题：

有意思的是，这个问题总是跟Javascript出现，实际上任何使用浮点数的语言都会有这个问题，也就是说，要是你在C或者Java里面用float和double类型，结果是一样的。另外有趣的是0.1+0.2其实不等于浏览器打印的0.30000000000000004，而是0.3000000000000000444089209850062616169452667236328125。

所以本文将会详细解释浮点数，而作为示例会试着分析上述的for循环和0.1+0.2现象。

使用科学计数法表示数字

在开始浮点数讲解之前，我们先了解下科学计数法，一般表示为一下形式：

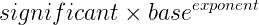
significant表示数字重要的数值部分，一般称之为尾数或者精度。尾数不包括0，0只是占位作用。Base则指定了数字系统的基数，如10进制的基数是10，二进制的基数是2。Exponent则决定了小数点要往左或者往右移动几位。

所有的数字都可以用科学计数法表示比方说：

指数为0意味着小数点不需要移动。0.00000022表示如下：

转化之后，我们就可以重新定义每个数字的部分了：

规范化科学计数法：

科学计数法可以理解为数字的浮点表示。“浮点”本来就意味着数字的小数点是可以浮动的。
另外根据科学计数法的特点我们会知道，规范化的科学计数写法对二进制数字来说，整数永远都是1。

IEEE 754浮点数

IEEE 754定义了很多关于浮点的运算，现在我们只对数字的存储，四舍五入和相加感兴趣。四舍五入是一个很频繁的操作，一般发生在选定的格式不够保存数字的时候。另外一篇文章有详细讲解二进制的四舍五入。了解其中的机制非常的重要。

现在我们来看看数字是怎么保存的吧~

理解数字的存储

标准规定的格式里面，最常用的是单精度和双精度两种。两者不同的地方在于占用的字节数和能表示的数字范围。将一个科学计数法表示的数字转化为IEEE754格式的算法适用于单精度和双精度，他们只是尾数和指数部分的位数不一样。

IEEE754浮点数分符号位，尾数和指数。双精度的格式是这么分配的（Javascript的数字类型）：

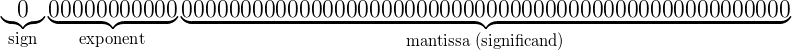
标志位1位，11位的指数以及52位的尾数。用表格这么表示：

指数使用偏移二进制存储，另一篇文章有详细的讲解

整数是如何存储的

来看看1是怎么表示
首先用科学计数法表示如下：

这样子我们便知道尾数是1，指数是0。得到这个信息之后，你可能觉得浮点表示如下：

事实如何呢？Javascript没有内置的函数可以直接让你看到数字的存储的位模式。于是我写了一个函数来打印数字的存储方式（在不考虑大小端的情况下。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
function to64bitFloat(number) {
    var i, result = "";
    var dv = new DataView(new ArrayBuffer(8));

    dv.setFloat64(0, number, false);

    for (i = 0; i < 8; i++) {
        var bits = dv.getUint8(i).toString(2);
        if (bits.length < 8) {
            bits = new Array(8 - bits.length).fill('0').join("") + bits;
        }
        result += bits;
    }
    return result;
}

调用这个函数，你就会知道1是这样存储的：

跟想象中的完全不一样啊，尾数部分没有数字，指数部分有很多1。为啥会这样呢？首先我们得知道所有数字都是从规范化的科学计数写法转化过来的。这么做有什么好处呢？如果小数点左边的数字永远是1的话，那么就不用浪费一位去保存它了，只需要在执行数学运算的时候，硬件把这个1补回来即可。因为1的小数点右边没有其他数，所以尾数部分我们没有东西可以保存，全是0。

现在看看指数部分的1是怎么来的。如上述提到的指数存储的偏移二进制，计算如下：

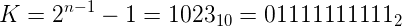
可以看到这就是上述表示中的值，所以0在偏移二进制的确是这么保存的。如果还不清楚的话，可以查看我的另外一篇文章。

现在让我们尝试用上面学到的东西来试着对3进行浮点表示把。二进制中3表示为11，规范化之后就是：

小数点之后只有一个数字是1，上述可知小数点右边的1是不存储的，同时根据规范化的结果可以知道指数部分是1。接着算一下1的偏移二进制怎么表示吧：

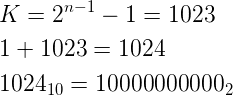
另外一点需要注意的是，尾数部分数字按照科学计数法的表示的顺序放置–即从小数点开始从左到右依序填入。综上所述，用浮点数表示3为：

用我前面提供的函数会得到一样的结果哦。

为什么0.1+0.2不等于0.3

既然我们知道数字是如何保存的，接下来讨论下这个经典的问题。标准的解答如下：

二进制里面带分母的分数只有2的倍数才能被有限的表示。因为0.1的分母是10，0.2的分母是5都不是2的倍数，所以这些数字不能被有限小数表示。为了以IEEE 754浮点数保存这些小数，不得不把这些尾数进行四舍五入，半进度的10位，单精度的23位，双精度的52位。根据不同的精度位数，浮点数会把0.1和0.2转化比其数学表示大或者小的数。正因为如此0.1+0.2总是不等于0.3

这个解释对一些开发者来说已经够了，但更好的方式是搞清楚底层到底发生了什么。这就是我们现在要做的事情。

将0.1和0.2进行浮点表示

先看看0.1的浮点表示。首先需要做的事是转化0.1为二进制，一直乘以2即可：

接着用规范化的科学计数法表示它：

由于尾数只有52位，于是我们得把无限循环的小数做四舍五入

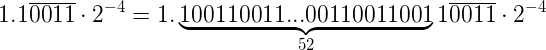
最后一件事，计算-4的偏移二进制表示：

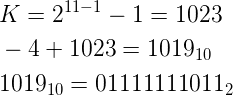
于是0.1的浮点表示为：

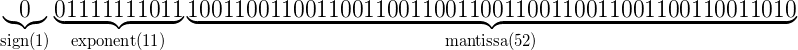
0.2的浮点表示建议自己实践下哈~

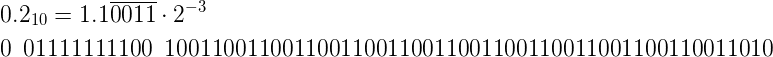
计算0.1+0.2的结果

将上述数字从浮点表示转为科学计数法表示的话，得下面的结果：

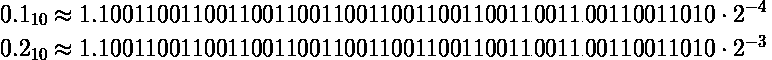
要将两数相加的话，需要先将指数部分转为相等。

相加可得：

我们需要用浮点表示了相加的结果，所以接下来只需要将他规范化，四舍五入（如果需要的话），计算偏移二进制即可：

规范化之后发现超过52位了，我们需要做一次四舍五入：

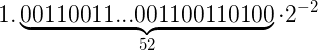
最终的浮点表示为：

这就是当你计算0.1+0.2的时候保存的准确结果。为了得到这个结果，计算机做三次四舍五入，保存每个数字各一次，保存结果一次。而单纯的保存0.3的时候，只做了一次四舍五入。正是四舍五入导致了0.1+0.2的结果跟0.3的表示不一致。当Javascript执行0.1+0.2===0.3的时候，实际上做了按位比较，因为结果不同，自然就返回false了。而0.1和0.2在二进制中不用被有限表示，四舍五入总是存在，故0.1+0.2永远都不会等于0.3。

为什么for循环会停不下来？

理解for循环为什么死循环的关键是9007199254740991。这个数字非常的特殊，以至于他有自己的常量表示，下面是EcmaScript标准关于其的描述：

Number.MAX_SAFE_INTEGER是一个最大的数字n以至于n+1都可以准确表示一个数字值。Number.MAX_SAFE_INTEGER等于9007199254740991（2⁵³−1）

MDN是这么解释的：

常量中的safe指的是能准确表示和比较的整数，譬如Number.MAX_SAFE_INTEGER + 1 === Number.MAX_SAFE_INTEGER + 2会得到true，而这从数理角度是不对的。

首先需要明确的一点是，它不是js能表示的最大的数，比如数字9007199254740994即MAX_SAFE_INTEGER + 3也能被安全的表示。如果要找最大能表示的数字的话，因为用Number.MAX_VALUE（等于1.7976931348623157e+308）这个常量。令人惊讶的是，在MAX_SAFE_INTEGER和MAX_VALUE之间有许多数字不能被表示。实际上在MAX_SAFE_INTEGER和MAX_SAFE_INTEGER+3之间就有一个数字不能被表示：9007199254740993。如果你把这个数输入console中，你会发现它等于9007199254740992。

为了理解到底发生了什么，我们先看看9007199254740991 (MAX_SAFE_INTEGER)的浮点表示：

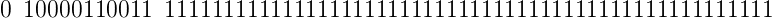
转为科学计数法表示为：

右移小数点52位得：

也就是为了保存MAX_SAFE_INTEGER，指数为52的情况下，我们用光了尾数所有的位数来表示它。由于所有位都被用了，要表示更大的数字只能把指数增加1。指数变为53的话，我们得把小数点右移53位，由于尾数只有52位，我们只能在最后添加0补充了,所以指数54就需要补2个0，55就要3个，依次类推。

这会有什么影响呢，也许你已经猜到了。由于所有大于MAX_SAFE_INTEGER的数，我们会以0结尾，那就意味着没有奇数能被浮点表示了！

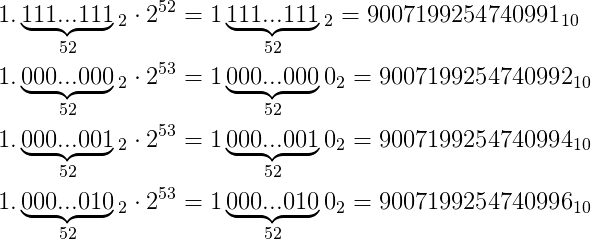
能看到9007199254740993和9007199254740993都不能被64位的浮点数表示。如果你继续试下去便会发现不能表示的数字会有偶数出现！而随着指数的增加，不能表示的范围会越来越大！

死循环

再看看for循环：

1
2
3
for (var i=1; 1/i > 0; i++) {
    console.log("Count is: " + i);
}

它不会停下来，上面提到了以为1/i的结果不是一个整数，而是浮点数。现在你已经知道浮点数和Number.MAX_SAFE_INTEGER了，应该很容易理解为啥它不会停止循环。

如果要循环结束的话，只有i必须变成Infinity， 因为1/Infinity > 0 是false。 当然这永远不会发生。上面的章节我解释了为啥一些数字不能被表示，以及他们被四舍五入为最近可表达的偶数。当i增加到9007199254740993的时候(也就是MAX_SAFE_INTEGER+2)，由于最后一位数字无法表示，于是只能四舍五入到9007199254740992。于是循环便卡在这两个数字之间了。

关于NaN和Infinity的几句话

我决定对NaN和Infinity做一点简述作为文章的结束。NaN意味着Not a Number，它和Infinity不一样，尽管他们都被当初浮点操作的特殊例子去处理。它们的指数是1024（即11111111111），而Number.MAX_VALUE的指数是1023（即111111111101）。

由于NaN是用浮点表示的，所以当你看到typeof NaN返回number的时候，应该不会惊讶了吧。哦，对了，它的尾数有一个1：

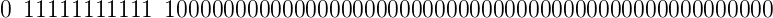
有许多数学操作都会得到NaN的结果，例如0/0或者Math.sqrt(-4)。Javascript中有一些函数也会返回NaN，譬如parseInt。而有意思的地方是，所有和NaN的比较操作都会返回false。例如下面的操作都会得到false：

1
2
3
4
5
6
7
NaN === NaN
NaN > NaN
NaN < NaN

NaN > 3
NaN < 3
NaN === 3

只有NaN是不等于自身的，要检查一个值是不是NaN的话，得调用isNaN函数。

Infinity则是另外一个浮点表示中设计来用处理溢出和一些数学操作的特殊用例，譬如1/0。Infinity表示如下：

正的Infinity符号位是0，负的Infinity是1。MDN有一篇文章介绍了一些得到Infinity的操作。和NaN不同的是，Infinity可以很安全的用于比较操作。

原文地址： https://medium.com/dailyjs/javascripts-number-type-8d59199db1b6